El cálculo es una rama de las matemáticas que se ocupa del estudio de las tasas de cambio y acumulación. Es una herramienta fundamental en diversas áreas como la física, la economía y la ingeniería. El Teorema Fundamental del Cálculo es uno de los conceptos más importantes en esta disciplina, ya que establece una relación fundamental entre el cálculo diferencial y el cálculo integral.
El Teorema Fundamental del Cálculo establece que la derivada de una función es igual a la integral de esa función. En otras palabras, nos permite calcular el área bajo una curva utilizando el cálculo integral. Este teorema es esencial para resolver problemas de optimización, encontrar áreas y volúmenes, y modelar fenómenos físicos y económicos.
En este artículo, exploraremos en detalle el Teorema Fundamental del Cálculo y su importancia en el campo del cálculo. Descubriremos cómo se aplica en diferentes situaciones y cómo podemos utilizarlo para resolver problemas complejos. ¡Prepárate para revelar el poder del cálculo!
Principio de Torricelli
El Principio de Torricelli es un concepto fundamental en la física y la hidrodinámica que establece que la velocidad de salida de un fluido a través de un orificio en un recipiente es proporcional a la raíz cuadrada de la altura del fluido sobre el orificio. Este principio fue descubierto por el científico italiano Evangelista Torricelli en el siglo XVII y es una consecuencia directa de la ley de conservación de la energía.
El Principio de Torricelli se puede aplicar a una amplia variedad de situaciones, desde el flujo de líquidos en tuberías hasta el movimiento de gases en conductos. En el caso de un líquido, la velocidad de salida del fluido a través del orificio se puede calcular utilizando la fórmula v = √(2gh), donde v es la velocidad de salida, g es la aceleración debida a la gravedad y h es la altura del fluido sobre el orificio.
Este principio tiene importantes aplicaciones en la ingeniería y la física, ya que permite calcular la velocidad de salida de un fluido en diferentes situaciones. Por ejemplo, se puede utilizar para determinar la velocidad de salida de agua de una tubería o la velocidad de salida de un gas de un conducto. Además, el Principio de Torricelli también se utiliza en la construcción de fuentes y en la medición de caudales en ríos y canales.
Introducción al Teorema Fundamental del Cálculo
El Teorema Fundamental del Cálculo es uno de los conceptos más importantes en el campo de las matemáticas y tiene una amplia aplicación en diversas áreas, como la física, la economía y la ingeniería. Este teorema establece una relación fundamental entre el cálculo integral y el cálculo diferencial, permitiendo calcular áreas bajo una curva y encontrar la función primitiva de una función dada.
El Teorema Fundamental del Cálculo consta de dos partes: la primera parte establece que si una función es continua en un intervalo cerrado y tiene una función primitiva en ese intervalo, entonces el valor de la integral definida de la función en ese intervalo es igual a la diferencia entre los valores de la función primitiva evaluada en los extremos del intervalo. En otras palabras, la integral definida de una función continua en un intervalo puede ser calculada mediante la evaluación de la función primitiva en los extremos del intervalo.
La segunda parte del teorema establece que si una función es continua en un intervalo cerrado y su integral definida en ese intervalo es igual a cero, entonces la función es constante en ese intervalo. Esto significa que si la integral definida de una función continua es cero en un intervalo, entonces la función no varía en ese intervalo.
Definición del Teorema Fundamental del Cálculo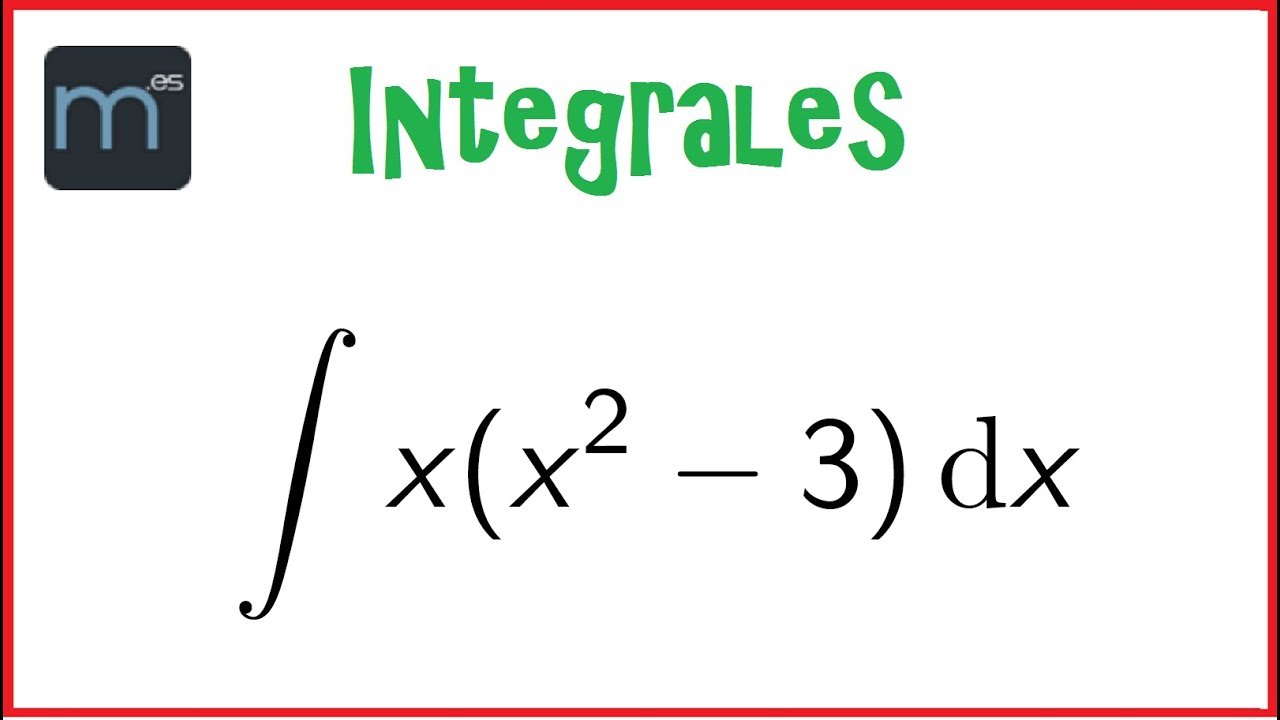
El Teorema Fundamental del Cálculo es uno de los conceptos fundamentales en el estudio del cálculo integral. Este teorema establece una relación entre la derivación y la integración de una función, y proporciona una herramienta poderosa para calcular áreas bajo una curva y encontrar antiderivadas.
En términos simples, el Teorema Fundamental del Cálculo establece que si una función f(x) es continua en un intervalo [a, b] y F(x) es una antiderivada de f(x) en ese intervalo, entonces el valor de la integral definida de f(x) desde a hasta b es igual a la diferencia entre los valores de F(x) evaluados en los extremos del intervalo, es decir:
∫ab f(x) dx = F(b) – F(a)
Este teorema es esencial en el cálculo integral, ya que permite calcular áreas bajo una curva al encontrar la antiderivada de una función y evaluarla en los extremos del intervalo. Además, el Teorema Fundamental del Cálculo establece una conexión profunda entre la derivación y la integración, demostrando que son operaciones inversas una de la otra.
Aplicaciones del Teorema Fundamental del Cálculo
El Teorema Fundamental del Cálculo es una herramienta fundamental en el estudio del cálculo integral. Este teorema establece una relación entre la derivación y la integración, y tiene numerosas aplicaciones en diferentes áreas de las matemáticas y la física.
Una de las aplicaciones más comunes del Teorema Fundamental del Cálculo es el cálculo de áreas bajo una curva. Gracias a este teorema, podemos determinar el área encerrada entre una función y el eje x mediante la integración de la función en un intervalo dado. Esto es especialmente útil en problemas de geometría y física, donde necesitamos calcular áreas de regiones irregulares.
Otra aplicación importante del Teorema Fundamental del Cálculo es el cálculo de volúmenes de sólidos de revolución. Este teorema nos permite encontrar el volumen de un sólido obtenido al girar una región acotada alrededor de un eje. Mediante la integración de la función que describe la región, podemos determinar el volumen exacto del sólido.
Prueba del Teorema Fundamental del Cálculo
El Teorema Fundamental del Cálculo es uno de los conceptos más importantes en el campo de las matemáticas y tiene una amplia gama de aplicaciones en diferentes áreas. Este teorema establece una relación fundamental entre la derivación y la integración, y nos permite calcular áreas bajo una curva y encontrar antiderivadas de funciones.
La prueba del Teorema Fundamental del Cálculo se basa en dos partes: la primera parte establece que si una función es continua en un intervalo cerrado y tiene una primitiva en ese intervalo, entonces la integral definida de la función en ese intervalo es igual a la diferencia entre los valores de la primitiva en los extremos del intervalo. La segunda parte establece que si una función es continua en un intervalo cerrado y su integral definida en ese intervalo es cero, entonces la función es constante en ese intervalo.
Para demostrar la primera parte del teorema, se utiliza el concepto de la función primitiva o antiderivada. Si una función tiene una primitiva en un intervalo, entonces la integral definida de la función en ese intervalo se puede calcular simplemente restando los valores de la primitiva en los extremos del intervalo. Esto se debe a que la derivada de una función primitiva es igual a la función original. Por lo tanto, la integral definida de la función es igual a la diferencia entre los valores de la primitiva en los extremos del intervalo.
Relación entre el Teorema Fundamental del Cálculo y la derivada
El Teorema Fundamental del Cálculo es uno de los conceptos fundamentales en el estudio del cálculo integral. Este teorema establece una relación profunda entre la integral definida y la derivada de una función. En pocas palabras, nos permite calcular el área bajo una curva y también encontrar la función original a partir de su derivada.
La relación entre el Teorema Fundamental del Cálculo y la derivada se puede entender de la siguiente manera: si tenemos una función f(x) y su derivada F'(x), entonces la integral definida de F'(x) en un intervalo [a, b] nos dará el valor de F(b) – F(a), es decir, la diferencia entre los valores de la función primitiva F(x) en los puntos a y b.
Esta relación es extremadamente útil en muchas áreas de la ciencia y la ingeniería. Por ejemplo, en física, podemos utilizar el Teorema Fundamental del Cálculo para calcular el trabajo realizado por una fuerza variable a lo largo de una trayectoria. En economía, podemos utilizarlo para calcular el área bajo una curva de oferta y demanda y determinar el excedente del consumidor o del productor.
Teorema del Valor Medio para Integrales
El Teorema del Valor Medio para Integrales es una importante herramienta en el cálculo que establece una relación entre el valor promedio de una función en un intervalo y su integral definida en ese intervalo. Este teorema es una consecuencia directa del Teorema Fundamental del Cálculo y tiene aplicaciones en diversas áreas de las matemáticas y la física.
De acuerdo con el Teorema del Valor Medio para Integrales, si una función continua f(x) está definida en un intervalo cerrado [a, b], entonces existe al menos un punto c en ese intervalo donde el valor promedio de la función es igual a su integral definida en ese intervalo. Matemáticamente, esto se expresa como:
f(c) = \frac{1}{b-a} \int_{a}^{b} f(x) dx
Este teorema es especialmente útil para determinar valores promedio de una función en un intervalo dado. Además, puede ser utilizado para demostrar otros resultados importantes en el cálculo, como el Teorema del Valor Medio para Derivadas.
Teorema del Valor Medio para Derivadas
El Teorema del Valor Medio para Derivadas es un resultado fundamental en el cálculo diferencial. Este teorema establece que si una función es continua en un intervalo cerrado [a, b] y derivable en el intervalo abierto (a, b), entonces existe al menos un punto c en el intervalo (a, b) donde la derivada de la función es igual a la razón de cambio promedio de la función en el intervalo [a, b].
En términos más simples, el Teorema del Valor Medio para Derivadas nos dice que si una función tiene una tasa de cambio promedio constante en un intervalo, entonces en algún punto dentro de ese intervalo la tasa de cambio instantánea (la derivada) será igual a esa tasa de cambio promedio.
Este teorema es muy útil en el análisis de funciones y en la resolución de problemas de optimización. Nos permite encontrar puntos críticos donde la derivada se anula, lo que indica máximos o mínimos locales de la función. Además, el Teorema del Valor Medio para Derivadas es una herramienta fundamental en la demostración del Teorema Fundamental del Cálculo, que establece la relación entre la integral y la derivada de una función.
Teorema del Valor Medio Generalizado
El Teorema del Valor Medio Generalizado es una extensión del Teorema del Valor Medio del Cálculo Diferencial. Este teorema establece que si una función f(x) es continua en un intervalo cerrado [a, b] y derivable en el intervalo abierto (a, b), entonces existe al menos un punto c en el intervalo (a, b) donde la derivada de la función es igual al cociente de la diferencia de los valores de la función en los extremos del intervalo y la diferencia de los valores de los extremos del intervalo.
En términos más simples, el Teorema del Valor Medio Generalizado nos dice que si una función es continua en un intervalo cerrado y derivable en el intervalo abierto, entonces en algún punto dentro del intervalo la tasa de cambio promedio de la función será igual a la tasa de cambio instantánea en ese punto.
Este teorema es de gran importancia en el cálculo, ya que nos permite encontrar valores específicos de una función en un intervalo dado. Además, es utilizado en la demostración del Teorema Fundamental del Cálculo, que establece la relación entre la integral y la derivada de una función.
Teorema del Valor Medio para Funciones Vectoriales
El Teorema del Valor Medio para Funciones Vectoriales es una importante herramienta en el cálculo que nos permite entender el comportamiento de una función en un intervalo dado. Este teorema establece que si una función vectorial es continua en un intervalo cerrado y diferenciable en el intervalo abierto, entonces existe al menos un punto en el intervalo abierto donde la derivada de la función es igual al cambio promedio de la función en el intervalo cerrado.
En otras palabras, si tenemos una función vectorial que describe una trayectoria en el espacio, el Teorema del Valor Medio nos dice que en algún punto de esa trayectoria, la velocidad instantánea en ese punto será igual a la velocidad promedio en todo el intervalo de tiempo considerado.
Este teorema es muy útil en diversas aplicaciones, como por ejemplo en la física, donde nos permite determinar el momento en el que un objeto en movimiento alcanza una velocidad determinada. También es utilizado en la economía, para analizar el crecimiento de una variable en un periodo de tiempo dado.
Teorema del Valor Medio para Ecuaciones Diferenciales
El Teorema del Valor Medio para Ecuaciones Diferenciales es una herramienta fundamental en el estudio de estas ecuaciones. Este teorema establece una relación entre el valor promedio de una función en un intervalo y la derivada de esa función en algún punto dentro de ese intervalo.
En términos más precisos, si tenemos una función diferenciable f(x) en un intervalo [a, b], entonces existe al menos un punto c en ese intervalo donde la derivada de la función en ese punto es igual al cociente de la diferencia entre los valores de la función en los extremos del intervalo y la longitud del intervalo. Matemáticamente, esto se expresa como:
f'(c) = \frac{f(b) – f(a)}{b – a}
Este teorema es especialmente útil para demostrar resultados importantes en el análisis de ecuaciones diferenciales. Por ejemplo, se puede utilizar para demostrar la existencia de soluciones a ciertos problemas de valor inicial, o para establecer propiedades de las soluciones de ecuaciones diferenciales.
Teorema del Valor Medio para Series de Potencias
El Teorema del Valor Medio para Series de Potencias es una herramienta fundamental en el cálculo que nos permite encontrar valores específicos dentro de una serie de potencias. Este teorema establece que si tenemos una función representada por una serie de potencias, entonces existe al menos un valor en el intervalo de convergencia de la serie donde la función alcanza un valor específico.
Para entender mejor este teorema, consideremos una función f(x) que está representada por la serie de potencias:
f(x) = a₀ + a₁x + a₂x² + a₃x³ + …
Donde los coeficientes a₀, a₁, a₂, … son constantes y x es la variable independiente. El Teorema del Valor Medio para Series de Potencias nos dice que si f(x) es continua en un intervalo [a, b], entonces existe al menos un valor c en ese intervalo donde:
f'(c) = a₁ + 2a₂c + 3a₃c² + … = 0
En otras palabras, la derivada de la función en ese punto específico es igual a cero. Esto implica que en algún punto dentro del intervalo [a, b], la función alcanza un máximo o mínimo.
Este teorema es de gran utilidad en el cálculo, ya que nos permite encontrar valores específicos dentro de una serie de potencias. Además, nos proporciona información sobre la concavidad de la función y la existencia de puntos críticos. En resumen, el Teorema del Valor Medio para Series de Potencias nos revela el poder del cálculo al permitirnos analizar y comprender mejor las funciones representadas por series de potencias.
Puedes leer para más conocimiento sobre Teorema de los Triángulos